Der vorliegende Text soll als Einstieg in die Thematik dienen und möglichst leicht verständlich sein, weshalb die Sachverhalte teilweise deutlich vereinfacht dargestellt werden. Dies soll nicht unterstellen, dass eine ausführliche Beschäftigung mit der Thematik nicht sinnvoll und oder gar nicht notwendig für eine angemessene Anwendung sei, jedoch könnte eine ausführlichere Darstellung der Formeln und Hintergründe jeweiliger Maße zur Berechnung der Intraklassenkorrelation zum Einstieg aufgrund der hohen Komplexität ggf. abschreckend und irreführend auf den/die Leser*in wirken. Für eine intensivere Beschäftigung mit der Thematik empfehle ich das (meiner subjektiven Ansicht nach) sehr ausführlich geschriebene Buch Beurteilerübereinstimmung und Beurteilerreliabilität von Wirtz und Caspar (2002) auf das ich mich überwiegend beziehen werde.
Für die Berechnung der Interraterreliabilität intervallskalierter Daten wird einheitlich die Intraklassenkorrelation (ICC) empfohlen.
Aber was heißt das Wort „Intraklassenkorrelation“ eigentlich?
Intra = Innerhalb…is klar oder?
Klassen = hier: die herangezogenen Daten bzw. Variablen „gehören einer einzigen gemeinsamen Klasse an –> im Klartext: sie stimmen in ihrer Metrik und Varianz überein (Scherm, 2014; wo wir wieder beim Thema Testvoraussetzung wären), d.h. sie Urteilen über ein und dasselbe Subjekt, innerhalb eines latenten Merkmals (ein Merkmal ist hier im Grunde eine Abhängige Variable, AV) oder einer Dimension oder psychometrischen Skala (oder was auch immer) „varianzhomogen“. Mehr zur Varianzhomogenität weiter unten im Text. Die Rater stammen also vereinfacht ausgedrückt aus einer „Klasse“.
Korrelation = Zusammenhangsmaß
Zusammengesetzt heißt das: Die Intraklassenkorrelation ist ein Zusammenhangsmaß, was Auskunft darüber erteilen soll, wie sehr sich zwei oder mehr Rater / Beurteiler (z.B. Psycholog*innen) innerhalb ihrer Urteile „einig“ sind, hinsichtlich der Merkmalsausprägung (z.B. Emotionsregulation) eines Subjekt (z.B. eines Kindes) – sofern sie einer Klasse angehören (ihre Varianzen homogen sind). Damit schätzt die Intraklassenkorrelation die Zuverlässigkeit (Reliabilität) eines beliebigen Beurteilers ein (Wirtz & Caspar, 2002).
Was unterscheidet die Intraklassenkorrelation von dem einfachen Zusammenhangsmaß der Pearson (Produkt-Moment) Korrelation?
Die ICC berücksichtigt Unterschiede hinsichtlich der Streuung und Mittelwerte zwischen den Beurteilern und kann im Gegensatz zur Produkt-Moment Korrelation auch für mehr als zwei Rater / Beurteiler berechnet werden. Darüber hinaus wirken sich Mittelwertsunterschiede auf das Ergebnis der ICCunjust reliabilitätsmindernd aus (Wirtz & Caspar, 2002; Scherm, 2014).
Welche Voraussetzungen liegen der Berechnung der ICC zugrunde?
Wenn man sich die Formel der ICC in Ruhe zu Gemüte führt, wird schnell klar: es geht um das Prinzip der Varianzzerlegung (within-subjekt und between-subject,…). Daher sollten für die Berechnung der ICC im Prinzip dieselben Voraussetzungen gegeben sein wie für die Varianzanalyse.
- Intervallskalenniveau der AV (prüfen über: Antwortformat),
- UV ist kategorial (hier sind es ja unterschiedliche Rater, also nominal) und deren Stufen sind unabhängig,
- Ansatzweise Normalverteilung der AV (bei hinreichend großer Stichprobe kann jedoch vom zentralen Grenzwertsatz und damit einer relativen Robustheit des Tests hinsichtlich der Verletzung dieser Voraussetzung ausgegangen werden; prüfen über: Histogramm mit Normalverteilungskurve und Kolmogorov-Smirnov-Test für n > 50 oder Shapiro-Wilk-Test für n < 50),
- Varianzhomogenität zwischen den Stufen der Unabhängigen Variable (UV) ist gegeben (prüfen über: Levene-Test),
- Zusätzlich für das zweifaktorielle Modell: keine Interaktion zwischen den Ratern, sonst kann dies zu einer Unterschätzung der Reliabilität führen (prüfen über: Zweifaktorielle Varianznalyse / im Rahmen der ICC-Berechnung über den Tukey-Additivitätstest)
- Es sollten mindestens 10 Subjekte (im Idealfall alle von denselben Beurteilern) beobachtet worden sein (ab 3 Subjekten jedoch keine Fehlermeldung mehr in SPSS)
…obgleich sich – zumindest für das einfaktorielle Modell (mehr dazu weiter unten im Text) – angeblich lediglich für n < 10 unter der Verletzung der Voraussetzungen Normalverteilung und Varianzhomogenität Reliabilitätsverfälschungen zeigen (Scherm, 2014).
Okay, wir halten fest: ziemlich viele Voraussetzungen, die vor der eigentlichen Berechnung der ICC geprüft werden sollten. Die Berechnung der ICC erfolgt später im Text, zunächst erstmal die Theorie. 🙂
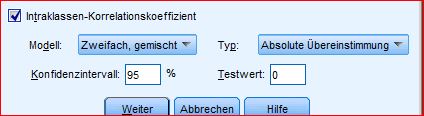
Da meine Autodidaktik-fördernden Grafiken über die gewöhnlichen WordPress-Funktionen nicht so hübsch aussehen, geht es nun in einem PDF-Dokument weiter…bitte hier öffnen: Söhnen, S. A. (2019). Einstieg in die Intraklassenkorrelation
Viel Spass beim Lesen, Sarah